En la entrada Capacidades Analíticas IBM SPSS Statistics señalábamos que las técnicas de análisis estadístico se desarrollan con la finalidad de identificar, cuantificar y explicar los efectos sistemáticos que algunos factores tienen sobre el comportamiento de un determinado fenómeno. En el ejemplo que usaremos en esta entrada, se trata de determinar si el tratamiento con aspirina tras un infarto de miocardio disminuye o no la probabilidad de fallecer. Este objetivo debe aticularse a través de un diseño experimental adecuado, donde se divide un determinado conjunto de individuos infartados en 2 grupos: el denominado de tratamiento (a los que se suministra aspirina tras el infarto) y el de control (a los que se suministra placebo). La asignación de cada individuo a uno u otro grupo se hace de forma aleatoria con la finalidad de eliminar sesgos de selección que pudieran comprometer la validez de las conclusiones del estudio.
Frecuentemente los resultados del experimento son cuestionados, lo que conduce a nuevos estudios con la finalidad de refrendar o refutar la evidencia alcanzada previamente, lo que va generando un corpus incremental de resultados de experimentos (no todos necesariamente idénticos aunque si deben permitir la cuantificación de un mismo efecto) que es susceptible de "consolidarse" bien para obtener estimaciones más precisas del efecto, bien para entender que covariables -que necesariamente deben tomar diferentes valores entre los estudios considerados- influyen (y cómo) sobre el efecto en causa.
Este proceso de consolidación de estudios diferentes, donde la unidad de análisis ya no son los individuos de los estudios originales, sino los propios estudios en sí, se conoce como meta-análisis (sin que ello se pueda tomar como una definición rigurosa). Dependiendo de lo que se mida (variables continuas o binarias) y cómo se haga (datos brutos originales o estimaciones de efecto de cada estudio), el meta-análisis comprende un conjunto de técnicas y tests estadísticos que puede requerir la aplicación a las "observaciones" -ahora necesariamente retrospectivas- de algunos supuestos (como, por ejemplo, que se comporten según determinados modelos probabilísiticos ) con la finalidad de permitir modelizar la variación entre las estimaciones de los efectos de los diferentes estudios y obtener resultados tanto del tamaño del efecto como de su significatividad estadística. "Encajar" tamaños del efecto estimados en diferentes estudios dentro de un modelo probabilistico a partir del cual obtener ciertas conclusiones puede, a su vez, requerir realizar algunas transformaciones sobre los resultados de los estudios.......
Sí, el meta-análisis es al análisis, lo que la meta- lingüística es a la lingüística.... todos los hablantes (analistas) pueden conversar (analizar) aplicando las reglas que le son propias, pero abordar la meta- lingüística requiere algunas consideraciones y cautelas. En el caso del meta-análisis tales consideraciones se refieren a cómo identificar la población o universo de estudios sobre los que meta-analizar, cómo muestrearla para evitar sesgos de selección (es particularmente conocido el sesgo de publicación que es la constatacion de que los estudios de efecto inconclusivos tienden a no ser publicados de forma que estan infrarepresentados en el conjunto de estudios disponibles para análisis), cómo ponderar las diferentes estimaciones de efecto en una estimación combinada , y un largo etcétera que no abordaremos aquí porque requiere una extensión muy superior a la de una entrada de blog.
Lo relevante es que la versión 28 de IBM SPSS Statistics incluye procedimientos para conducir meta-analisis tanto de variables binarias como continuas, sobre datos brutos o estimaciones del tamaño del efecto, así como la meta-regresión, técnica especialmente apropiada cuando se pretende estimar y entender cómo condiciones cambiantes entre los diferentes estudios analizados, recogidas a traves de covariables, afectan al tamaño del efecto. Adicionalmente, SPSS Statistics permite la estimación acumulativa del tamaño del efecto caso se disponga de una variable, por ejemplo la fecha, que permita ordenar criteriosamente tal acumulación de evidencia.
Como anticipamos, vamos a trabajar con un conjunto de datos que procede de Fleiss JL (1993): "The statistical basis of meta-analysis. Statistical Methods in Medical Research", 2, 121–45 y que contienen los resultados de diferentes estudios sobre el efecto de reducción de la mortalidad debido al tratamiento con aspirina en pacientes tras haber sufrido un infarto de miocardio. Consideraremos 7 estudios cuyos datos constan en el gráfico siguiente:
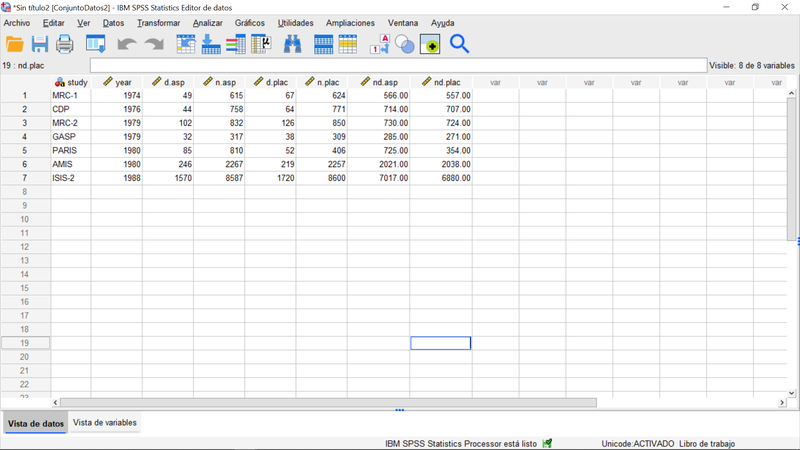
Se trata de un fenómeno binario (fallecimiento o no) para dos grupos (tratamiento mediante aspirina o placebo). Los datos son brutos, los recuentos de fallecimiento o no en cada grupo para cada estudio. Vamos a realizar un meta-analisis del tamaño del efecto, medido a través del estadistico de "Riesgo Relativo" que, en este caso, compara el riesgo de un resultado -fallecimiento o no dependiendo como se codifique- cuando se recibe tratamiento versus ese resultado sin tratamiento. RR = 1 significa que no hay efecto de tratamiento.
A partir de los datos anteriores -que es sencillo reproducir debido a su tamaño- donde el prefijo "d" significa fallecimiento, "nd" no fallecimiento, el sufijo "asp" aspirina y el "plac" placebo, y siendo que los datos son recuentos, es posible consolidar las estimaciones a través de la opción del menú Analizar>Meta-análisis>Resultados Binarios>Datos en Bruto para, a continuación, realizar las elecciones que se reflejan en el siguiente cuadro de diálogo:
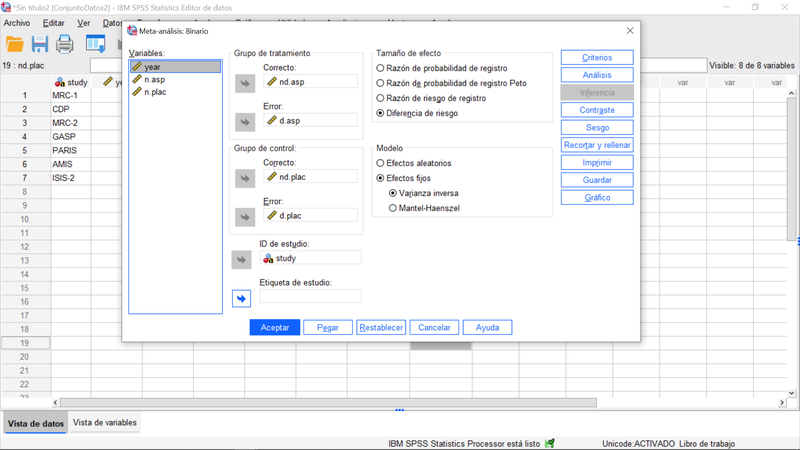
La combinación de resultados se concreta a través de modelos de efectos fijos (porque en este caso estamos asumiendo efectos comunes para todos los estudios). Otro escenario sería el correspondiente a un modelo de efectos aleatorios (asume que las estimaciones de los efectos varían entre estudios debido a la variación dentro de cada estudio y entre estudios -heterogeneidad).
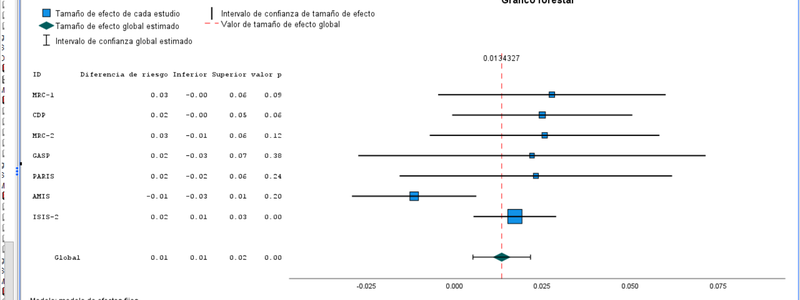
En la pestaña de gráficos del menú de meta-análisis vamos a especificar el llamado grafico forestal, que representa los intervalos de confianza de las estimaciones del efecto de los diferentes estudios, como ilustra la próxima imagen:
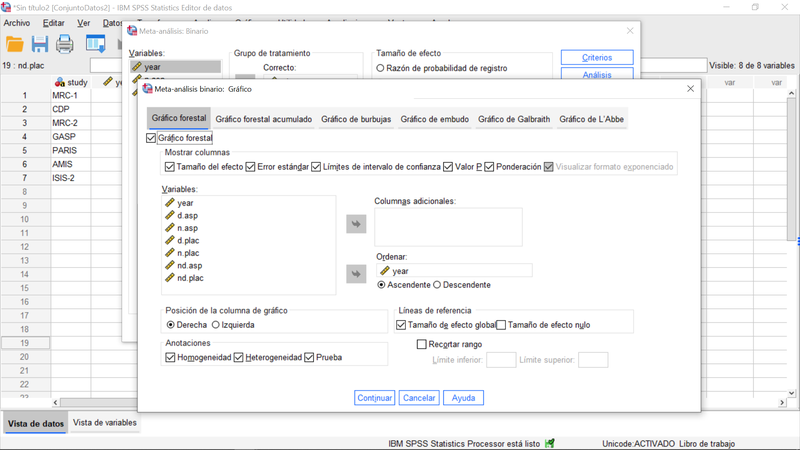
Pulsando continuar y aceptar, nos conduce al visor de resultados o al Libro de Trabajo, según hayamos configurado este modo en las opciones (menú principal, Editar>Opciones, separador general).
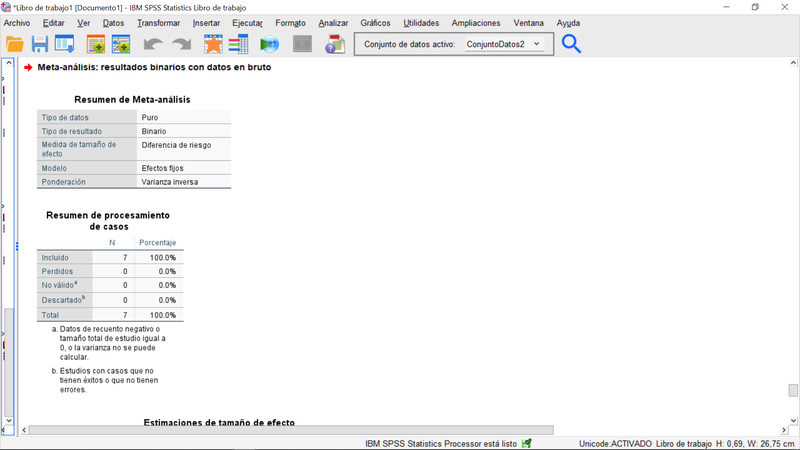
Las tablas resumen del procedimiento reflejando lo especificado y el gráfico forestal donde se pueden identificar los diferentes estudios, el tamaño del efecto estimado para cada uno de ellos, su intervalo de confianza (configuración por defecto 95%), y el efecto global. En este caso, el efecto global indica que hay un efecto positivo del tratamiento (la aspirina reduce la frecuencia relativa de fallecimiento frente al placebo), si bien una inspección del gráfico forestal y los datos originales (más arriba) permiten apreciar que el
último estudio considerado domina la estimación combinada.
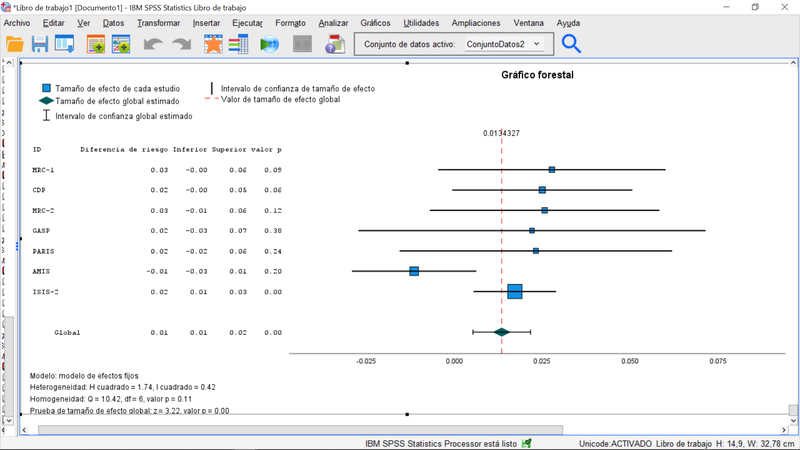
En todo caso, bajo el gráfico, el test Q de Homogeneidad nos indica que no podemos rechazar la hipótesis nula de que el tamaño del efecto es el mismo en todos los estudios.