Ocupémonos ahora de la POTENCIA de un contraste de hipótesis: la probabilidad de rechazar correctamente la hipótesis nula (porque es falsa, siendo cierta la aternativa).
Al final de la entrada anterior señalamos que es deseable trabajar con tests estadísticos que minimicen la probabilidad de rechazar hipótesis verdaderas y maximicen la probabilidad de rechazar hipótesis falsas. Como enseguida ilustraremos a través de un ejemplo gráfico, la potencia de un contrase -al igual que el nivel de significación- depende del tamaño de la muestra: lógicamente a mayor tamaño muestral mayor información disponible y menores serán las probabilidades de error al decidir entre hipóteses competidoras.
Imaginemos que un partido político -de creación reciente,-se presenta a las elecciones y, en medio de la campaña electoral, contrata nuestros servicios para contrastar la hipótesis de que están consiguiendo la intención de voto de una parte del electorado.
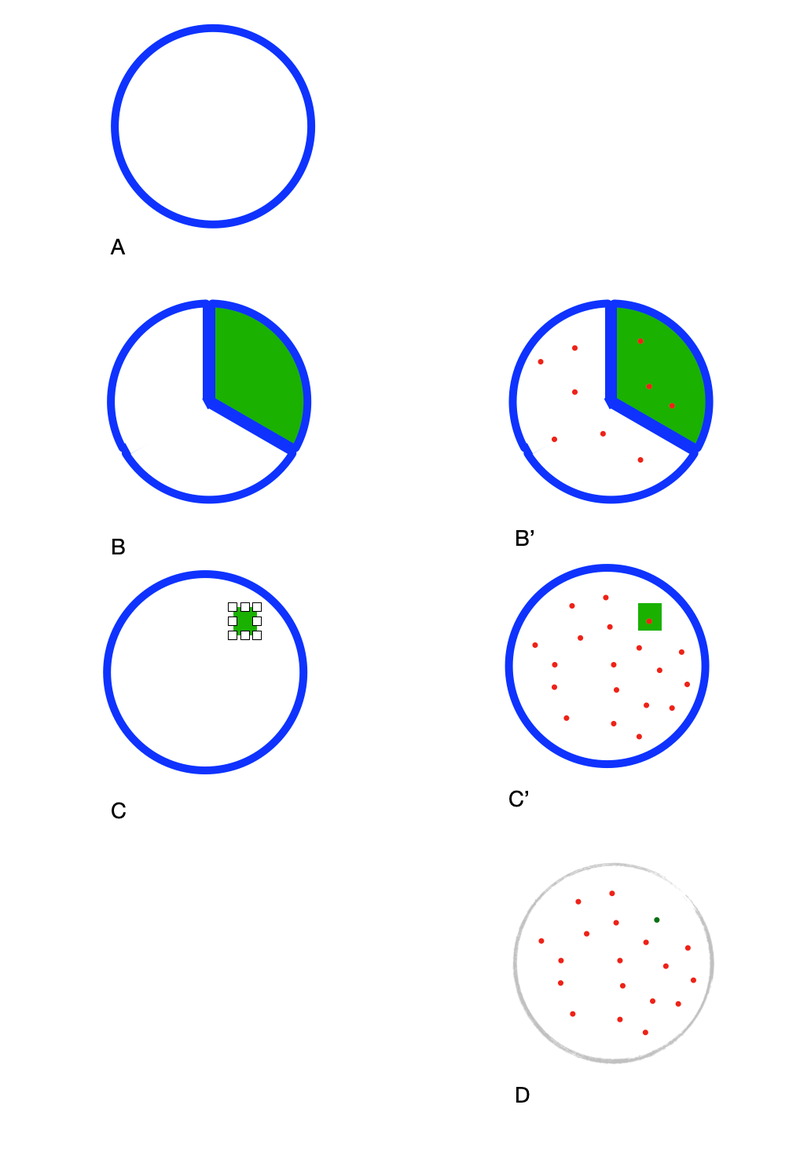
La columna de la izquierda de la ilustración anterior representa el estado del mundo real que, en condiciones normales, es desconocido para el encuestador. El círculo representa el universo de electores y la mancha verde los votantes favorable al partido en cuestión. El primer círculo A refleja la situación pre-campaña, cuando el partido aún no existía y no tenía votantes potenciales. Los círculos B y C representan 2 situaciones hipotéticas sobre el efecto que ha podido tener la campaña en la intención de voto. B supondría la captación de 1/3 del electorado y C un porcentaje menor: 5% o 1/20.
Imaginemos que deseamos contrastar que la intención de voto ha alcanzado por lo menos el "verde%" (tome verde el valor que sea). Para ello tomaremos una muestra de votantes y les preguntaremos sobre su intención de voto; lo que sería más o menos equivalente a disparar aleatoriamente sobre el círculo y ver la proporción de disparos que han dado en el área verde para tomar una decisión (los que se inclinan a votar al partido que contrata nuestros servicios), representados en B' y C' por los puntos sobre los círculos para decidir si se sostiene la hipótesis o no. La hipótesis nula que definimos es H0: p= "verde%" y la alternativa H1: < "verde%". La potencia del contraste, la probabilidad de rechazar la hipótesis nula cuando es falsa es evidentemente diferente en los escenarios hipotéticos B' (H0: p=33%) y C' (H0 : p=5%). En otras palabras, la Potencia del Contraste depende del tamaño del efecto que haya en la población; el área verde representa el efecto "cambio en la intención de voto" debido a la causa "campaña electoral". Si suponemos que tomamos muestras repetidas (disparos sobre el círculo) en las situaciones B' y C', cabe esperar que la frecuencia con que aparecerán resultados en la mancha verde sea inferior en C' que en B' y a menor frecuencia relativa de disparos en el verde menor probabilidad de aceptar la hipótesis de que el efecto es "verde%".
Por otro lado, C' ilustra el hecho de que si queremos capturar la mancha verde entre los "disparos", vamos a tener que disparar más veces que en B', de forma que la probabilidad de captar en el contraste un efecto que realmente existe -potencia- dado un determinado tamaño del efecto poblacional, aumenta con el tamaño de la muestra.
Por último, el círculo D ilustra lo que observaríamos en la "realidad" tras un muestreo concreto recreado por los puntos de color: un universo solo aproximadamente bien identificado y, bajo el supuesto de que el estado del mundo es el representado por C, un único disparo que alcanza la mancha verde. Este único disparo verde es, de hecho, el "efecto observado" o "efecto muestral" de la campaña electoral. Y será a partir del mismo que tendremos que decidir si tiene un tamaño "suficiente" para que nos inclinemos por "verde%" o no, lo que abordaremos en la siguiente entrada.
Lo expuesto ilustra la necesidad de incorporar los requisitos de potencia deseada a la hora de diseñar un experimento (o encuesta); concretamente cuando se va a definir el tamaño muestral si no queremos desperdiciar recursos en muestreos que no controlan o garantizan las probabilidades de error.
IBM SPSS Statistics ofrece un conjunto de procedimientos de"Análisis de Potencia" como la primera del menú principal "Análisis".
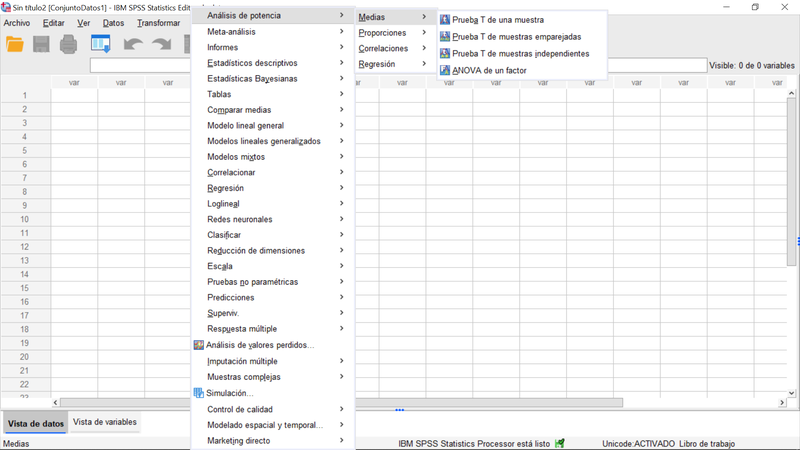
Dado que las probabilidades de error en la contrastación de hipótesis dependen de la variabilidad del fenómeno estudiado y esta última queda condicionada por el procedimiento o método de observación , es natural que haya procedimientos diferentes dependiendo del tipo de test y análisis del que se trate. IBM SPSS Statistics proporciona procedimientos para las medias (una o dos muestras, que pueden ser independientes o apareadas, y también para comparar las medidas de una variable condicionadas a más de dos niveles de un factor, a través del Análisis de la Varianza), para las proporciones (una muestra o dos relacionadas o independientes), coeficientes de correlación (Pearson, por rangos y parcial) o incluso para diseños relativamente simples de regresión lineal.
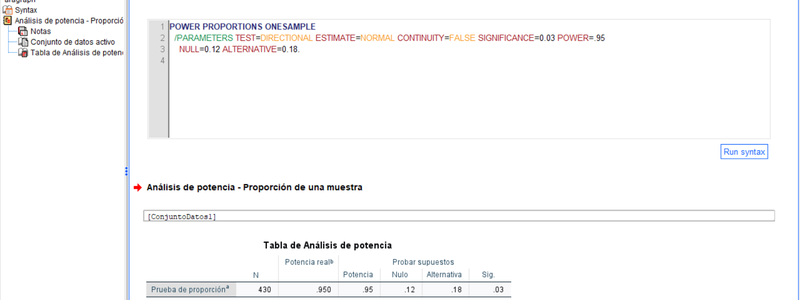
Por continuar con la lógica del ejemplo anterior, supongamos que el partido político en cuestión obtiene unos resultados del 12% y en las siguientes elecciones, convocadas a los pocos meses, quiere saber si la intención de voto se sitúa en ese momento en el 18% o más, frente al 12% de partida. Si deseamos contrastar H0: p=12% vs H1: p>=18%, fijando el nivel de significación en el 3% y la potencia deseada en el 95%, cuál sería el tamaño muestral necesario (?).
Analizar>Analisis de Potencia>Proporción de una muestra y fijemos las opciones como se muestra en la imagen siguiente
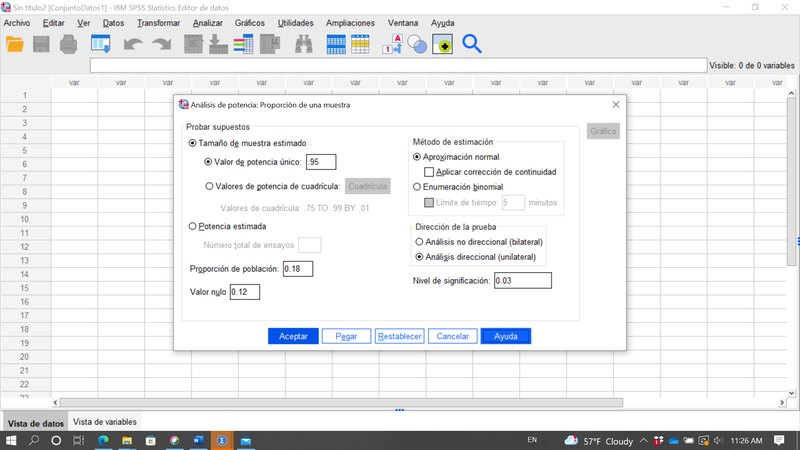
Hay varias opciones disponibles, de las que destacamos 2:
- queremos trabajar con un único valor de potencia o con un rango de valores, de forma que en lugar de obtener un tamaño muestral único obtengamos uno para cada nivel de potencia especificado.
- se trata de un contraste unilateral (como es el caso donde H1 es p>=18%) o bilateral (p podria ser mayor o menor que un valor dado).
Aceptando las especificaciones anteriorer, obtendríamos el siguiente resultado.
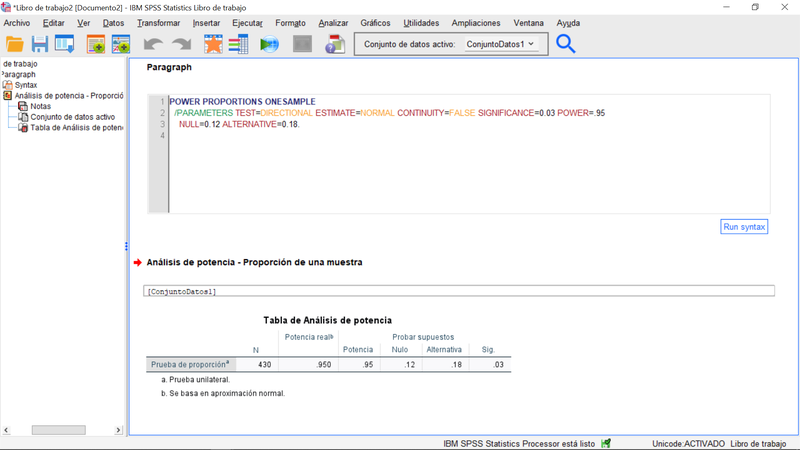
Por otro lado, si ya hubiésemos definido el tamaño muestral para esta prueba, por ejemplo en 125 casos, la imagen siguiente nos permitiria calcular cuál es la potencia de ese contraste.
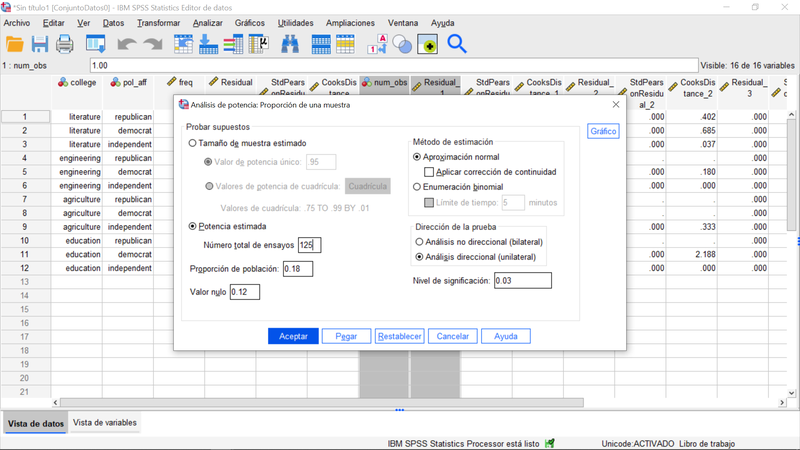
Sugerimos una mejor comprensión de estos procedimientos reejecute este procedimiento alterando las especificaciones.