Una tienda de productos on-line realizó un estudio experimental para saber los efectos de la configuración de un banner publicitario sobre las ventas de un producto nuevo atendiendo a dos factores: la colocación del banner en la ”landing page” con 3 opciones (parte superior, central, o inferior) y la “paleta de colores” empleada con dos opciones diferentes (pastel y vivos).
Es decir, queremos saber si existe un impacto sobre las ventas on-line de un producto en función de dos factores cuyos niveles (las diferentes opciones) vamos a analizar en su totalidad (la empresa ha decidido que no hay más opciones para la configuración del banner que las definidas anteriormente). Se trata de un ANOVA de 2 factores con efectos fijos que, además de apropiado para experimentos como el que nos ocupa, es de aplicación en estudios observaciones.
Como hay un total de 3*2=6 combinaciones de los factores, hablamos de 6 tratamientos.
Se consideraron 18 franjas horarias semejantes en cuanto a su duración al volumen de ventas y el tipo de clientes y cada una de estas franjas fue asignada aleatoriamente a uno de los 6 tratamientos, de modo que tendremos 3 observaciones en cada tratamiento, igualdad de tamaños que caracteriza al diseño del experimento como equilibrado. El periodo experimental fue de 3 días sin que, en este momento, profundicemos en los efectos que tales días puedan tener sobre las ventas. Los datos están recogidos en la tabla siguiente:
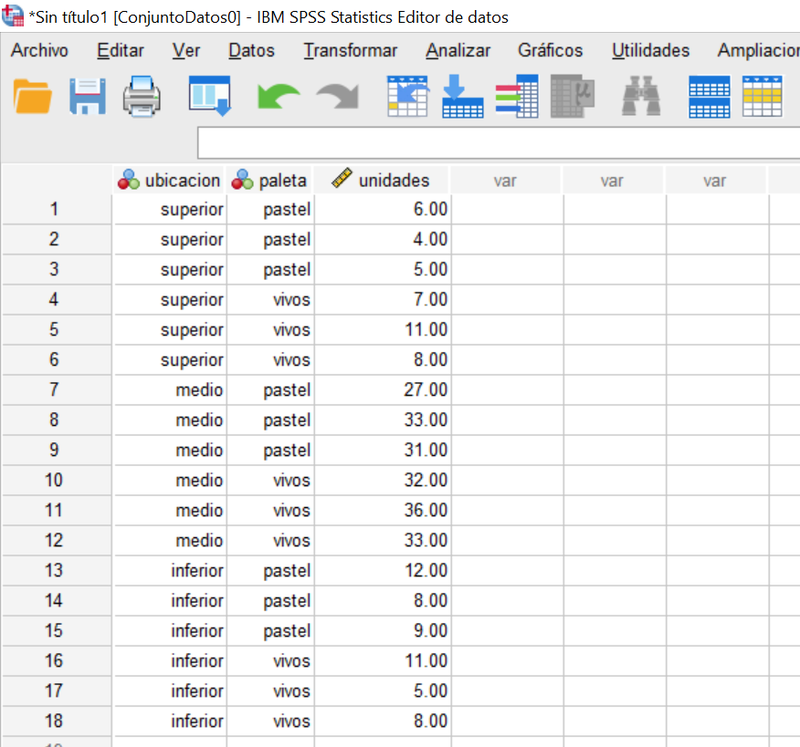
Para ejecutar el ANOVA vamos al menú principal de SPSS Analizar>Modelo lineal general>Univariado
Trasladamos “unidades” al recuadro para la variable dependiente.
Trasladamos Ubicación banner y Paleta colores al recuadro de factores fijos
No habiendo ningún factor aleatorio ni covariable presente (la edad referida a efectos ilustrativos en la píldora anterior -8- se acomodaría aquí ), y en ausencia de razones y variables para ponderar (por ejemplo para corregir la heterocedasticidad residual si fuera el caso) continuar....
Elegimos la opción modelo y especificamos como tal el Factorial Completa (incluye los efectos principales de los factores y las interacciones). Vemos que hay dos opciones para construir la expresión del modelo de forma flexible acomodando otros diseños (sin interacciones, o sólo entre determinados factores en el caso de análisis multifactorial).
En cuanto a la suma de cuadrados, IBM SPSS Statistics ofrece 4 opciones siendo el Tipo III la que consta por defecto. La descomposición de cuadrados Tipo I está afectada por el orden en el que los factores se incorporan al modelo y no toma en cuenta las interacciones entre factores, Tipo II elimina la limitación causada por el orden en que los factores entran en el modelo sin tener en cuenta las interacciones. Tipo III, por defecto, considera las interacciones y es independiente del orden. De todas formas en un diseño como el del ejemplo donde tenemos igual número de observaciones en cada tratamiento, las 3 son equivalentes como se puede concluir repitiendo los análisis con esta variación. Tipo IV se diseño para acomodar el caso de valores perdidos.
Marcamos la casilla de incluir la intersección, excepto que sepamos que los datos pasan por el origen.
Dejemos los contrastes para otro momento y vayamos al botón de gráficos
Trasladamos ubicación al recuadro eje horizontal
Trasladamos paleta al recuadro líneas separadas
Click en añadir, lo que nos permitirá apreciar los valores medios de unidades vendidas para cada nivel del factor ubicación, disponiendo en líneas diferentes los niveles del factor paleta. Enseguida veremos la utilidad de esta representación para analizar las posibles interacciones.
Dejemos los contrastes post hoc para otro momento: una vez confirmemos que existen efectos significativos de alguno de los factores, pues de lo contrario carece de sentido.
En el botón de medias marginales estimadas trasladamos ubicación y paleta al recuadro Mostrar medias para al tiempo que seleccionamos Comparar los Efectos Principales y ajustamos los intervalos de confianza de acuerdo con el nivel de significación apropiado a múltiples comparaciones, eligiendo el método de Bonferroni.
En el botón opciones elegimos Estadísticos descriptivos, estimaciones del tamaño del efecto, pruebas de homogeneidad, gráficos de dispersión versus niveles, gráficos de residuos, prueba de carencia de ajusto y el test de Breusch-Pagan para contrastar la homocedasticidad residual.
Click en aceptar para trasladarnos al visor de resultados:
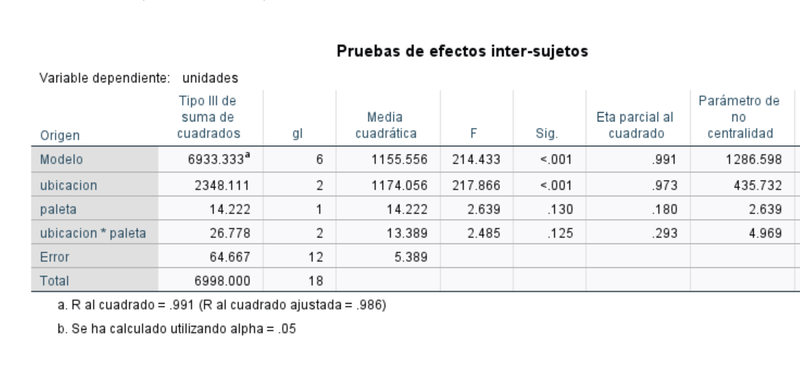
La tabla anterior muestra la descomposición de la suma de cuadrados totales entre sus partes componentes (factores, interaciones y error), sus grados de libertad correspondientes y su significatividad estadística mediante el correspondiente test F. Del análisis de la tabla se deduce que el modelo es globalmente significativo siendo que tanto e factor "paleta" como las interacciones paleta-ubicación carecen de significatividad estadística. La conclusión que se alcanza es: de los factores considerados solo la ubicación tiene un efecto diferenciador de la media de unidades vendidas.
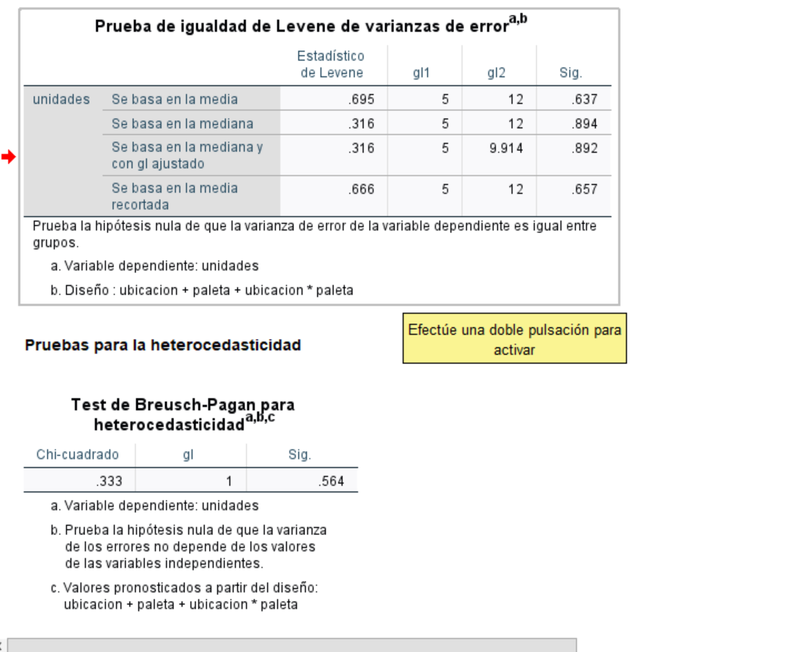
Para que esta conclusión sea válida deberemos verificar que los residuos presentan varianza constante. Los test son inequívocos en tal sentido, como se aprecia a continuación (los gráficos de los residuos no mostrados aquí apuntan en el mismo sentido).
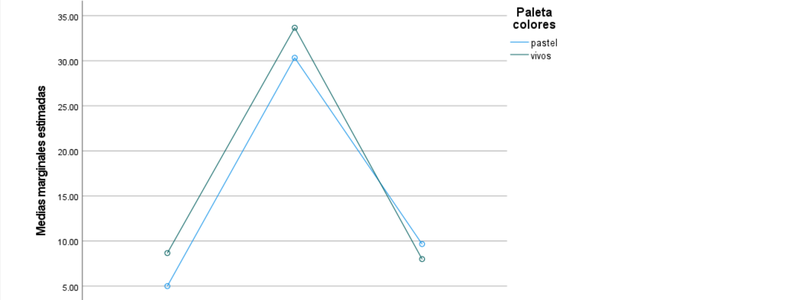
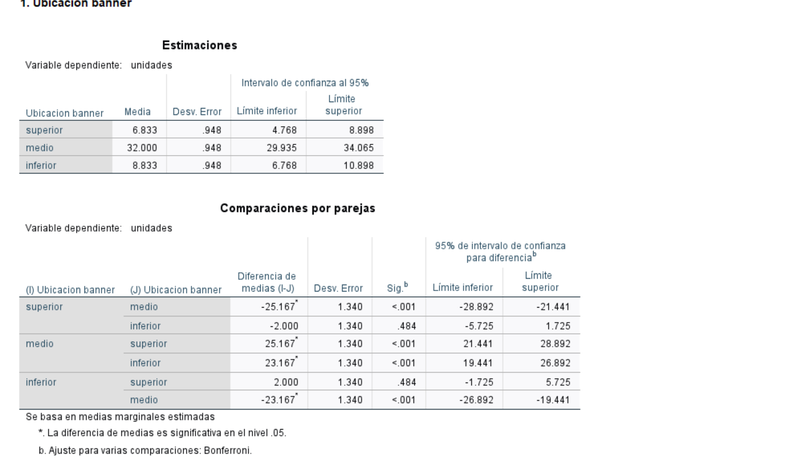
Las medias marginales estimadas para cada factor confirman (ver la sección de comparaciones por parejas) que es el factor ubicación y, concretamente, la ubicación en medio de la landing page la que muestra una media de ventas significativamente mayor que en las otras dos ubicaciones
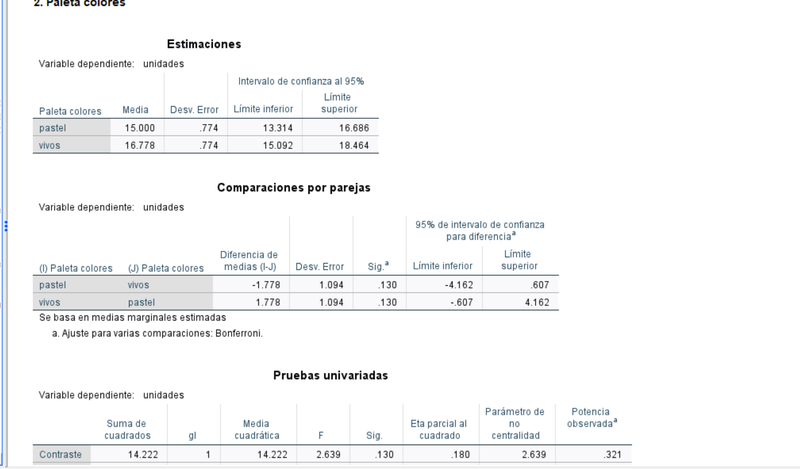
Mientras que el efecto de la paleta de colores es despreciable como se concluye del test univariante al final del gráfico precedente.
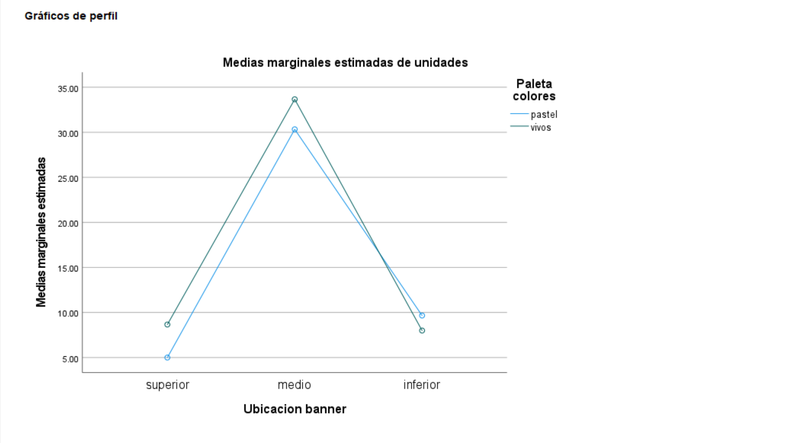
El gráfico de medias que ilustra esta entrada y que replicamos a continuación muestra claramente cómo la ubicación en medio de la landing page tiene un efecto significativo y positivo vs las ubicaciones alternativas. La interacción aparente (el cruce de ambas líneas) es evidentemente menor tanto en su expresión gráfica como debido al resultado del contraste sobre la interacción (tabla ANOVA al inicio).
Dejamos el detalle de la estimación del tamaño del efecto para la siguiente entrada de este blog.