Esta entrada es continuación de la anterior y se refiere al conjunto de datos y resultados allí tratados.
En la entrada anterior contrastamos un modelo factorial completo de efectos fijos con 2 factores y equilibrado, lo que quiere decir -respectivamente- que se consideraron todos los niveles de factores y sus interacciones, que no hay interés es analizar el efecto de otros niveles de los factores considerados que no estén presentes en el estudio (por ejemplo otras paletas de color o ubicaciones del banner) y que a cada tratamiento -combinación de niveles de los factores, a las que nos hemos referido como "subpoblaciones"- le fue asignado un número igual de unidades experimentales.
La conclusión del análisis anterior resultó ser que ni las interacciones ni el factor "Paleta de colores" tiene significatividad estadística. Es decir, el modelo inicialmente considerado para explicar la variación del número de unidades vendidas debe ser simplificado. El modelo factorial completo se expresa como:
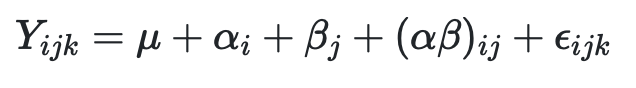
Donde los parámetros representan: mu la media global, alfa el efecto del nivel i del primer factor, beta el efecto del nivel j del segundo factor, alfa-beta la interacción entre ambos factores, y epsilon la variación aleatoria que suponemos constante. Esta especificación se conoce como modelo de celda, pues representa la observación k-ésima del tratamiento ij como el resultado aditivo de los términos anteriores.
El siguiente paso es ajustar un modelo factorial de efectos principales es decir, elminar las interacciones de la especificación anterior. En principio, dado que estamos trabajando con estimadores insesgados (propiedad de los métodos de estimación de modelo lineal general, minimos cuadrados o máxima verosimilitud) , la supresión del término interacción del modelo no afectará a las estimaciones puntuales de los efectos, aunque si a la estimación de la varianza residual pues, eliminadas las interacciones, los residuos del modelo son diferentes, así como sus grados de libertad.
A continuación indicamos las alteraciones que hay que hacer a la secuencia de especificaciones de la entrada anterior en menú principal de SPSS Analizar>Modelo lineal general>Univariado
En la opción "modelo" seleccionamos "construir términos" trasladando "ubicación" y "paleta" al recuadro del "Modelo". En el centro de la ventana, bajo "Construir términos" elegimos "efectos principales".
En "gráficos" eliminamos el de "ubicacion*paleta" en caso de que hayamos recuperado el cuadro de diálogo del análisis anterior. Trasladamos consecutivamente "ubicación" y "paleta" al área de "Eje horizontal" pulsando añadir después de cada selección -pues se trata de 2 gráficos diferentes-.
Dejando las restantes opciones como en la entrada anterior, click en aceptar para ajecutar el análisis.
La tabla siguiente confirma la significatividad del factor "ubicación banner" mientras que los colores no tienen efecto significativo sobre las ventas. Se aprecia igualmente que no se rechaza la hipótesis de homogeneidad de la varianza residual.
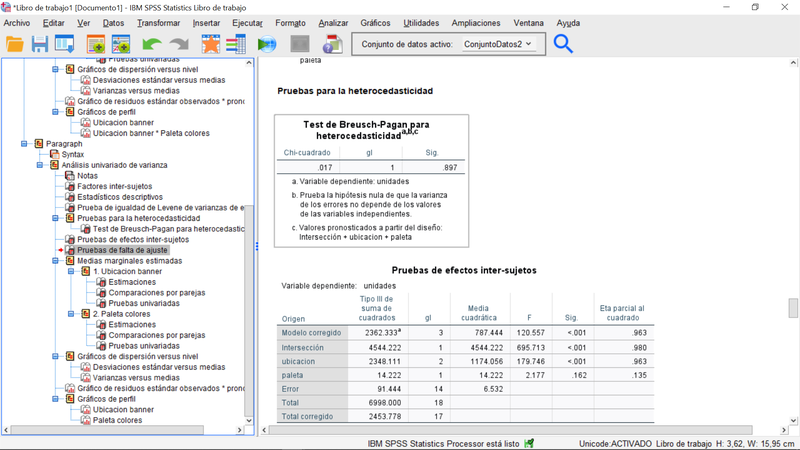
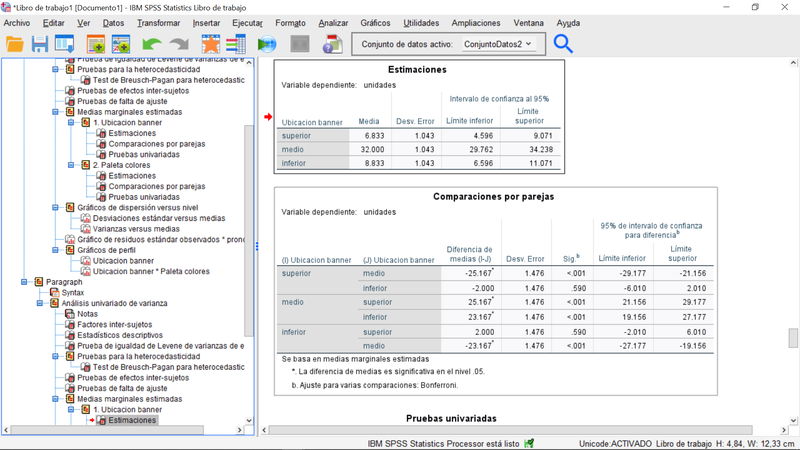
La tabla siguiente muestra las estimaciones de ventas medias para cada nivel del factor "ubicación banner". Como se ve, las estimaciones puntuales coinciden con las de la píldora anterior, si bien la desviación típica estimada es ahora ligeramente superior, lo que se traduce en intervalos de confianza ligeramente más amplios. Es el nivel "medio" de ubicación el que presenta una diferencia estadísticamente significativa versus situar el banner" en la zona "superior" e "inferior". Si comparamos esta tabla con la correspondiente a la especificación de la pildora anterior, vemos que los intervalos de confianza y por tanto, la estimación del efecto de cada nivel de este factor, son ligeramente mayores ahora, consecuencia del aumento de la variabilidad residual que es a su vez consecuencia de la reducción del número de parámetros del modelo lineal general (al eliminar el término interacción).
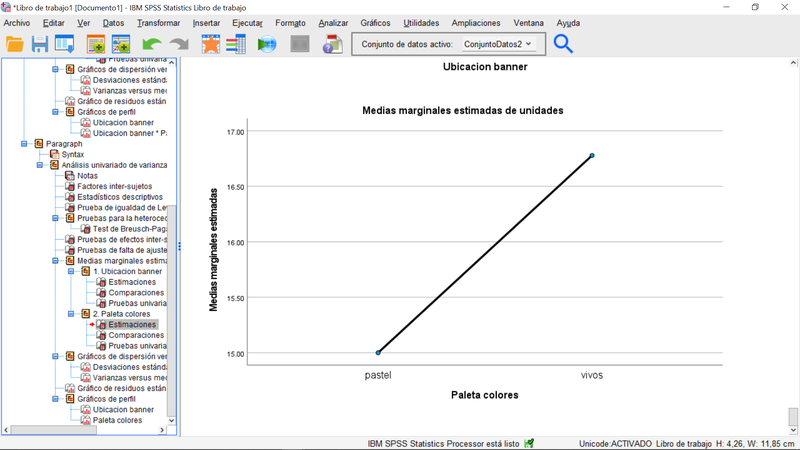
Mostramos a continuación el gráfico de las medias de ventas estimadas para cada nivel de la "Paleta de Colores". A pesar de la diferencia aparente, el efecto no tiene significación estadística. Si comprobamos en los resultados, las medias estimadas para los niveles "pastel" y "vivos" de la "paleta de colores" son, respectivamente, 15 y 16,7 unidades. Si la diferencia de 1,7 unidades vendidas fuese considerada de relevancia práctica, nuestro test estadístico tal cual ejecutado no sería suficientemente potente para detectarla. Esta es una ilustración oportuna de la diferencia entre la significatividad estadística y la significatividad (o relevancia) práctica de un efecto. sólo a través de un diseño correcto del experimento, se puede definir un test que tenga la potencia deseada para un determinado tamaño del efecto a detectar. La solución en este caso pasaría por aumentar el tamaño muestral mediante un procedimiento fundamentado en los conceptos revisados en las píldoras 5 a 7.
Admitiendo que el factor paleta no tiene efectos de interés práctico ni significatividad estadística, debemos reestimar nuestro modelo a un ANOVA de un factor único de efectos fijos. Esto lo podemos hacer a través del procedimiento Analizar>Comparar Medias>Anova de un factor o recuperando el cuadro de diálogo del análisis anterior eliminando simplemente el factor "paleta" en el cuadro de diálogo inicial y pulsando aceptar.
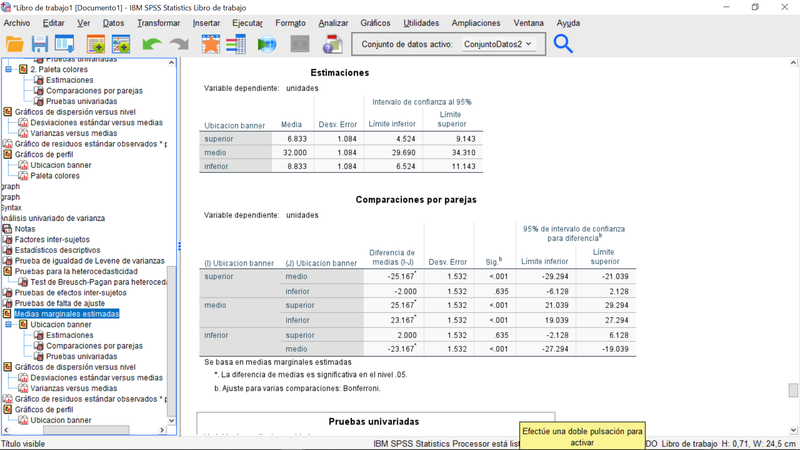
Los resultados son coherentes con los anteriores: la ubicación del banner en la zona media de la página tiene un efecto positivo sobre las ventas medias -en las franjas horarias de interés-. Concretamente entre 21 y 29 unidades más que cuando se situa en la zona superior, y entre 19 y 27 unidades más vs la zona inferior.

