Vamos a aprovechar los procedimientos explicados en la entrada anterior para abordar las bases conceptuales del análisis discriminante lineal que ilustraremos mediante un ejemplo práctico a partir de datos simulados:
En primer lugar, creamos un conjunto de n=200 observaciones procedentes de 3 grupos con distribución normal multivariante (5 variables). Las diferencias entre los grupos se deben a los valores medios de las variables, mientras que la estructura de covariación puede asumirse constante. En el bloque de código más abajo se explica la lógica de los pasos más importantes.
* semilla de aleatorización para replicar resultados. SET MTINDEX=1235. input program. + loop #i = 1 to 200. + do repeat response=r1 to r5 . + compute response = normal(1) . + end repeat. + end case. + end loop. + end file. end input program. correlations r1 to r5 / statistics=descriptives. * Extraemos los componentes principales mediante el procedimiento factor. * Producen 5 variables nuevas ortogonales . factor variables = r1 to r5 / print = default det /criteria = factors(5) /save=reg (all,pr). * mediante el comando matriz se define la matriz de correlaciones deseada, cor. * (como es arbitraria sugerimos repetir el procedimiento alterando los parámetros). * cho es la factorización de Cholesky de la matriz cor. * newx es la matriz 200*5 de nuevos datos que tiene como matriz * de correlaciones cor; se obtiene multiplicando la matriz de datos * transformados a partir de los componentes principales. matrix. get x / variables=pr1 to pr5. compute cor={1, -0.4, 0.3, -0.2, 0.1 ; -0.4, 1, 0.4, 0.3, 0.2 ; 0.3, 0.4, 1, 0.64, 0.3 ; -0.2, 0.3, 0.64, 1, 0.4 ; 0.1, 0.2, 0.3, 0.4, 1 }. compute deter=det(cor). print deter / title "determinante de la matriz de correlaciones" / format=f10.7 . print sval(cor) / title "descomposición en valores singulares de la matriz de correlaciones". print eval(cor) / title "autovalores de la matriz de correlaciones". * En una matriz simétrica sval y eigenvalues son idénticos. compute condnum=mmax(sval(cor))/mmin(sval(cor)). print condnum / title "número condición de la matriz de correlaciones" / format=f10.2 . compute cho=chol(cor). print cho / title "Factor Cholesky de la matriz de correlaciones" . * comprobamos la factorización de Chlesky. compute chochek=t(cho)*cho. print chochek / title "Factor Cholesky premultiplicado por su transpuesta" /format=f10.2 . compute newx=x*cho. save newx /outfile=* /variables= nr1 to nr5. end matrix. * Se crean 3 grupos de observaciones de forma aleatoria. * En cada grupo de definen las varianzas y medias mediante. * un cambio de origen y escala en las variables obtenidas por el. * procedimiento anterior. * Observar: dado que el cambio de escala aplicado determina. * la desviación típica de la variable resultante y las correlaciones. * fueron arbitrariamente establecidas mediante la matriz cor. * las covarianzas de la nuevas variables estan implicitamente determinadas. * En cada grupo se varian las medias y en menor medida las desviaciones. * típicas; ello afecta algo a las matrices de covarianzas pero. * no lo suficiente como para no poder asumir que la estructura de covariación. * es semejante dentro de los grupos. * Sugerimos probar con otros valores. COMPUTE grupo=RV.UNIFORM(0,3). DO IF (grupo <= 1). compute grupo=1. compute nr1=nr1*4 + 160. compute nr2=nr2*3 + 220. compute nr3=nr3*5 + 130. compute nr4=nr4*3 + 200. compute nr5=nr5*6 + 300. END IF. DO IF (grupo >1 AND grupo <= 2) . compute grupo=2. compute nr1=nr1*3.7 + 165. compute nr2=nr2*3.2 + 225. compute nr3=nr3*4.8 + 128. compute nr4=nr4*3.3 + 204. compute nr5=nr5*6.2 + 302. END IF. DO IF (grupo >2 AND grupo <= 3) . compute grupo=3. compute nr1=nr1*4.1 + 165. compute nr2=nr2*2.9 + 217. compute nr3=nr3*5.3 + 132. compute nr4=nr4*3 + 199. compute nr5=nr5*6.2 + 296. END IF. EXECUTE. correlations nr1 to nr5 / statistics=descriptives.
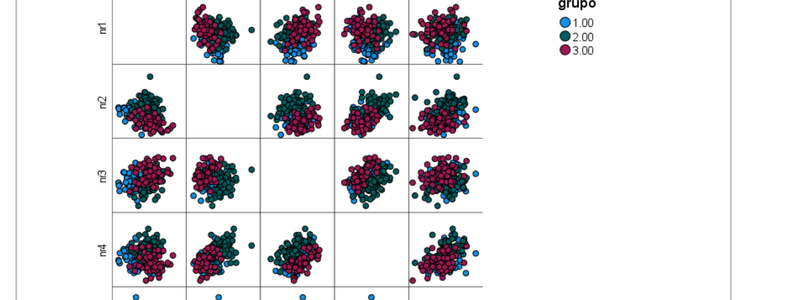
En segundo lugar, observamos la proyección de los elipsoides de las observaciones sobre los planos determinados por las variables originales tomadas de dos en dos. Se hace a través del menú de Gráficos, eligiendo en la Galeria el de "Dispersión Matricial" dentro de las opciones de "Dispersión/Puntos". Trasladamos "nr1 a nr5" al cuadro "Matriz de dispersión". En la pestaña "Grupos/ID de los Grupos" escogemos la opción "Variable de agrupación /apilado" y trasladamos la variable grupo al recuadro "establecer color". Aceptar nos traslada al resultado siguiente:
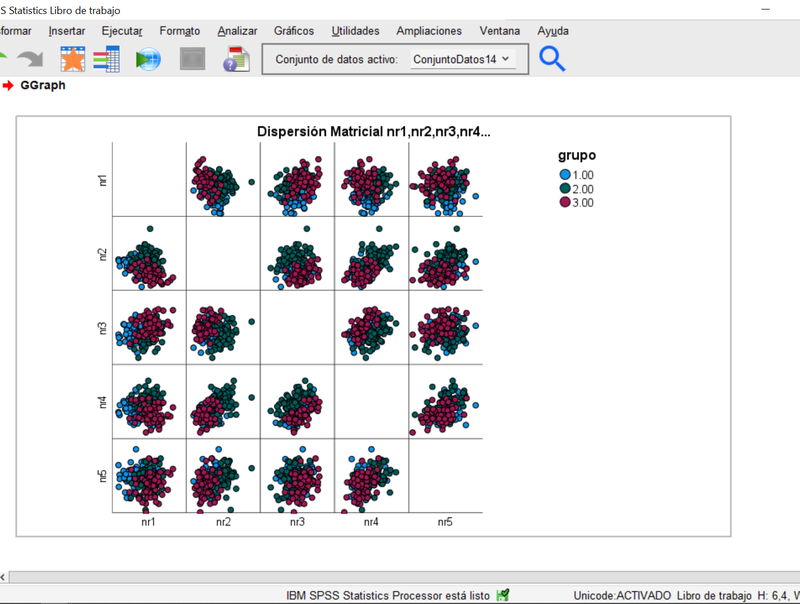
El gráfico anterior permite apreciar el solapamiento de las nubes de observaciones correspondientes a cada grupo, en cada uno de los planos bidimensionales posibes combinando las 5 variables (es una disposición de gráficos en una matriz simétrica, por lo que están duplicados).
En tercer lugar, el Análisis Discriminante Lineal se fundamenta en una técnica algebraica que busca, mediante la combinación lineal de las variables originales (nr1 a nr5), obtener unas nuevas variables (o dimensiones) que permitan maximizar -con respecto a estas nuevas variables- las diferencias entre los grupos. Es obvio que esta técnica, una vez entrenada sobre un conjunto de datos, puede servir como clasificador de observaciones en caso de disponer de información parcial. No es de extrañar que se use en el ámbito de la taxonomía de plantas y/o animales, entre otros casos de uso.
La idea bajo esta técnica es relativamente simple: supongamos que transformamos las observaciones de las 5 variables originales a través de una combinación lineal del tipo Yi= a1*nr1i + a2*nr2i+...a5*nr5i, donde i denota el número de caso (i:1,2...200 en nuestro ejemplo). Como cada observación (nr1i, nr2i...nr5i) pertenece a uno de los grupos 1 a 3, mediante esta combinación obtendríamos n valores Yi, i: 1..n, cada uno de los cuales estaría adscrito a uno de los 3 grupos originales. Dado que los Yi quedan determinados por la elección de los coeficientes (a1,...a5), nuestro objetivo es elegir estos coeficientes de modo que se maximicen las diferencias entre grupos.
En realidad, el procedimiento es ligeramente más complejo pues debemos considerar que obtendremos no una nueva variable, sino varias. La solución algebraica al problema es simple, las nuevas Ys (las nuevas variables) se obtienen a partir de los autovectores de la matriz resultate del producto Inv(W)*B; donde Inv(W) es la inversa de la matriz de covarianzas intra-grupos y B la matriz de covariazas entre-grupos. Los autovalores de esta matriz definen el cociente "varianza entre grupos/varianza intra grupos" de modo que la dimensión del auto-vector asociado al mayor autovalor, tiene el mayor poder discrimiante (de separación). Las variables Ys así obtenidas se denominan variables canónicas o también funciones discriminantes canónicas . El número máximo de variables canónicas es igual al mínimo (número de observaciones, número de grupos -1). En este ejemplo con 200 observaciones y 3 grupos, es 2.
Para realizar este análisis en IBM SPSS Statistics vamos al menú Analizar>Clasificar>Discriminante:
- Trasladamos grupo a la variable de agrupación, definiendo el rango 1 a 3
- Trasladamos las variables nr1 a nr5 al recuadro de variable independientes, dejando como método "Introducir independientes juntos"
- Click en "Estadísticos" y seleccionamos "Medias", todos los coeficientes de la función discrimiante y todas las matrices.
- En Clasificar indicamos "calcular según tamaño de grupos" , visualizando la "Tabla de resumen", "Clasificación dejando uno fuera", usamos la matriz "Intra-grupos" y escogemos el gráfico de "Grupos combinados".
Aceptar nos conduce al siguiente resultado gráfico:
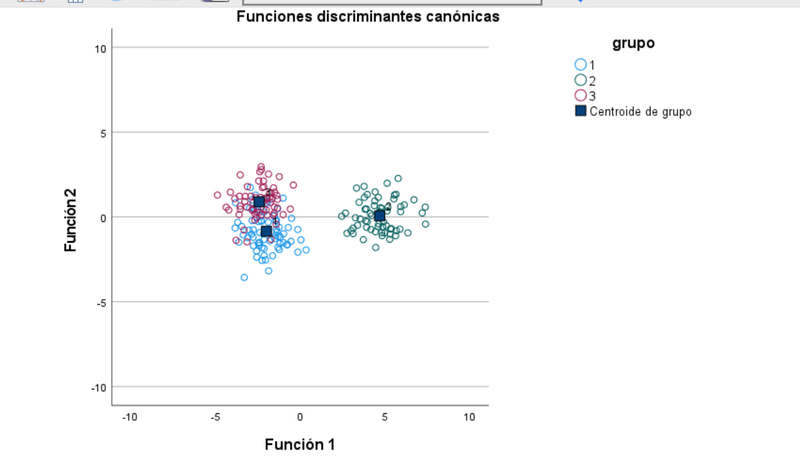
Se han extraido dos funciones discriminantes canónicas, como era previsto, que permiten diferenciar las observaciones con mayor claridad. Persiste un cierto solapamiento evidente entre los grupos 1 y 3.
En términos analíticos los coeficientes de la función discriminante (los a1,..a5 más arriba a los que se añade una constante para centrar las observaciones en el origen de las nuevas coordenadas) son:
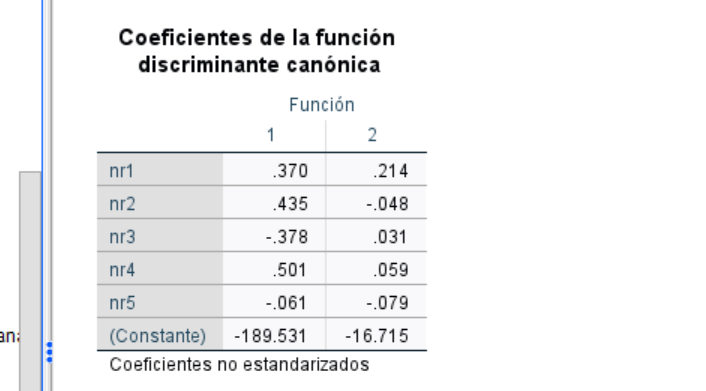
Dado que el procedimiento se basa en maximizar una cociente entre la varianza entre grupos y la intra grupos, el resultado puede quedar afectado tanto por que el numerador sea relativamente grande, como el denominador pequeño. Para controlar tal efecto, se pueden calcular los coeficientes estandarizados de modo que tengan varianza-dentro unitaria. Eso permitiría interpretar la contribución de cada variable original a la función discriminante y darle un sentido real. Como los datos son simulados, en este ejemplo no aplica. No obstante:
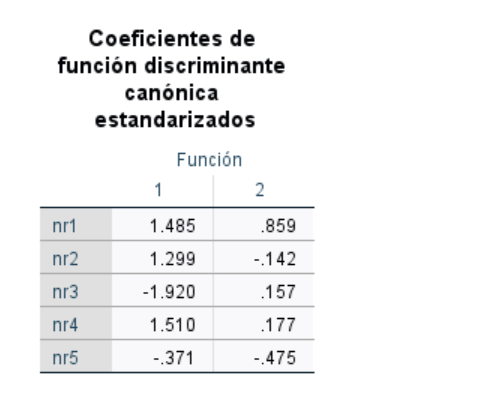
La capacidad discriminante relativa de cada una de los 2 funciones discriminantes se aprecia a través de los autovalores referidos anteiormente que, en el ejemplo son:

Lo que permite apreciar que la primera función trabaja considerablemente mejor que la segunda a efectos de separar las observaciones entre grupos.
Por último, para evaluar el desempeño de las funciones discriminantes como clasificadores, podemos mostrar la matriz de confusión. El 87% de las obserevaciones resultan bien clasificadas, que baja al 85.5% en validación cruzada.
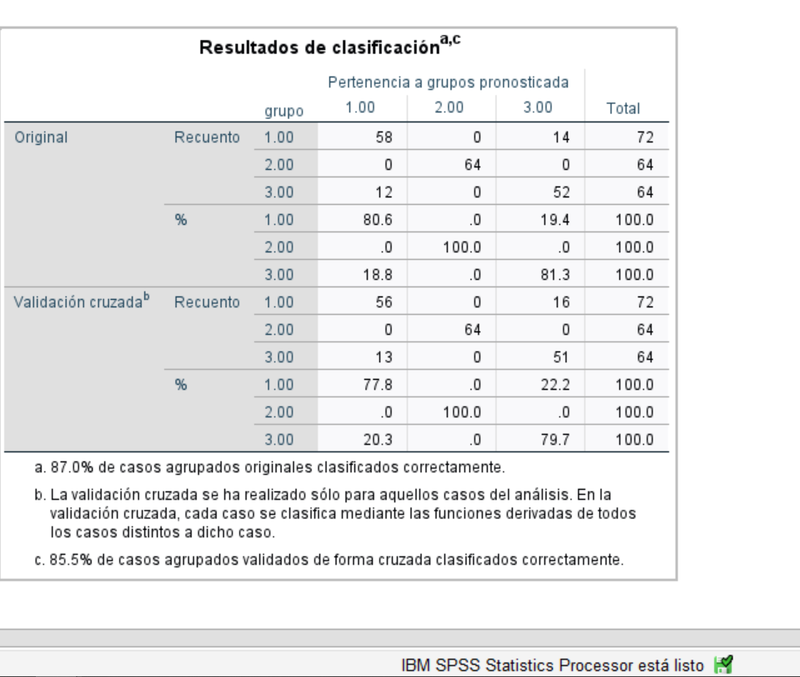
No hemos entrado en la parte inferencial de este análisis pues nuestro objetivo era repasar los conceptos fundamentales de esta técnica que se puede emplear de forma descriptiva para reducir la dimensionalidad de algunos conjuntos de datos.
Conviene no confundir este análisis con el de Componentes Principales cuyo objetivo es encontrar las dimensiones que maximizan la variabilidad de las observaciones y no entre grupos.